Datum og posisjonsformat
av Otto Milvang
Geografiske koordinater
Jorda roterer gjennom en akse som løper gjennom nordpolen og sydpolen. Denne aksen sammen med klodens sentrum er referanse for koordinatene. Sett fra verdensrommet ser jorda ut som en perfekt kule, men i virkeligheten er jorda litt sammentrykket ved polene og litt bredere ved ekvator. Eller mer matematisk: Jorda kan modelleres som en omdreinings-ellipsoide med en flattrykning på ca 1/300. GPS-systemet modellerer jorda med en WGS-84 ellipsoide.
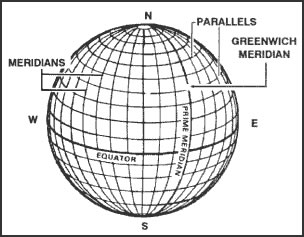
Vi kan trekke rette linje fra nordpolen til sydpolen. En slik linje kalles en meridian. Punkter som ligger med lik avstand til nordpolen eller sydpolen danner parallellsirkler eller paralleller.
Vi kan få oppgitt en posisjon, for eksempel N 59° 58.393 E 010° 39.346 H=473, og i et kartverk eller med en GPS kan vi finne dette punktet i naturen. Eksempelet over er en svært nøyaktig angivelse og som gir posisjon med bedre enn 2m nøyaktighet. Punktet beskrevet er trigpunktet på Kragstøtten i Oslo, et av Norges 925 førsteordens trigonometriske punkter. Men hva betyr egentlig tallene?
Nord/syd koordinaten angir breddegrad, og denne kan man måle ved å se på solhøyden kl 12:00 ved vårjevndøgn eller høstjevndøgn. Linja som angir en breddegrad er en parallell. Står sola rett over oss er vi på ekvator = 0 grader. Er sola i syd(nord) måler man antall grader fra rett opp og mot sola og får direkte ut hvilken nordlig(sydlig) breddegrad man er på. Er vinkelen man måler 90 grader betyr det at sola ligger helt i horisonten og vi er på nordpolen(sydpolen). I praksis måler man heller vinkelen mellom horisonten og sola. Breddegrad = 90 - måleverdi. Jorda deles inn i 180 breddegrader og nummereres fra S90° til N90°. Hver breddegrad kan deles i 60 breddeminutter, og hvert breddeminutt kan igjen deles i 60 breddesekunder. Fra gammelt av sa man at en nautisk mil = et breddeminutt = 1852m, men dette er ikke helt riktig. Ved ekvator er et breddeminutt ca 1843m og ved nordpolen er den 1862m. I gjennomsnitt er et breddeminutt 1852.216m, men en nautisk mil er likevel definert til å være nøyaktig 1852m (IHC, Monaco, 1929). Grunnen til at avstand mellom breddegrad varierer er at jorda ikke er helt rund, kombinert med at breddegrad er definert med solhøyde ved vår/høstjevndøgn, og ikke ved avstand til ekvator.
Øst/vest koordinaten angir lengdegrad. Det finnes ikke naturlig 0-punkt for lengdegrad, men fra 1884 bestemte man at en linje trukket fra nordpolen, gjennom Greenwich-observatoriet i London og videre ned til sydpolen skulle defineres som nullmeridianen. Relativt til denne nullmeridianen vil lengdegraden fortelle hvor mange grader man må sideveis i forhold til nullmeridianen. Lengdegrader er også meridianer. Punkter øst for Greenwich får østlig lengde, og punkter vest for Greenwich får vestlig lengde. Jorda deles altså inn i 360 lengdegrader og nummereres fra W180° til E180° (og W180° = E180° = datolinjen). Hver lengdegrad kan deles i 60 lengdeminutter, og hvert lengdeminutt kan igjen deles i 60 lengdesekunder. Lenden på et breddeminutt varierer med breddegrad. Ved ekvator er 1 lengdeminuttet = 1 breddeminuttet = 1843m, og ved nordpolen måtes alle lengdegrader, og lenden blir 0 på polpunktet. Generelt er lengden på 1 lengdeminutt = 1 breddeminutt * cos(breddegrad).
H angir ortometrisk høyde, eller det vi kaller "høyde over havet". Egentlig er ortometrisk høyde definert som høyde over geoiden. Geoiden er en flate der den ortometriske høyden er null, og når vi i eksempelet har H=473 betyr dette at hvis vi gravde en trang og svært dyp kanal fra Oslofjorden og inn mot Kragstøttten ville havnivået ligge 473m under oss. Geoiden påvirkes av landformasjonen. Det betyr at geoiden ikke er særlig lett å beskrive matematisk. En GPS kan måle høyde over en ellipsoide (WGS-84 ellipsoide), og i Norge ligger geoiden mellom 18m og 48m over ellipsoiden og med høeste avvik innerst i Sognefjorden. Man kan tenke seg dette som at Jotunheimen trekker vannet oppover. Laveste avvik har vi i Øst-Varanger. Gpsen har innebygde tabeller som korrigerer for dette avviket.
Rettvinklede koordinater
Selv om bredde og lengdegrader er en presis måte å angi en posisjon på er det mer hensiktsmessig å bruke koordinater med metriske enheter. Dette letter både avstandsberegning og arealberegning, i alle fall innenfor små lokale områder.
Vi kan få oppgitt en posisjon, for eksempel (-3480 6690) som kan være en alternativ skrivemåte for posisjonen til Krogstøtten. Med utgangspunkt i det gamle observatoriet i Oslo som fundamentalpunkt sier vi at vi kommer til Krogstøtten om man går 6690m nordover, og så tar en retning 90° til venstre (vestover) og går i den retningen 3480m. Legg merke til at man ikke følger rett vest hele veien fordi breddesirkler er sirkler, mens vi følger et rettvinklet system.
Den vanligste måten å konstruere et rettvinklet koordinatsystem på er å bruke en transvers mercator projeksjon. Om man tar en gjennomsiktig sylinder og trer utenpå jordkloden slik at den berører meridianen som går gjennom observatoriet i Oslo (eller en hvilken som helst annen meridian). Om man nå ser rett ovenfra kan man tegne landprofilen på sylinderen. Er man ganske nær sentralmeridianen blir dette ganske, men man ser at om man er svært langt fra sentralmeridianen blir landskapet svært fortegnet. I praksis er dette svært nøyaktig om man er innen 3° lengde fra sentralmeridianen.
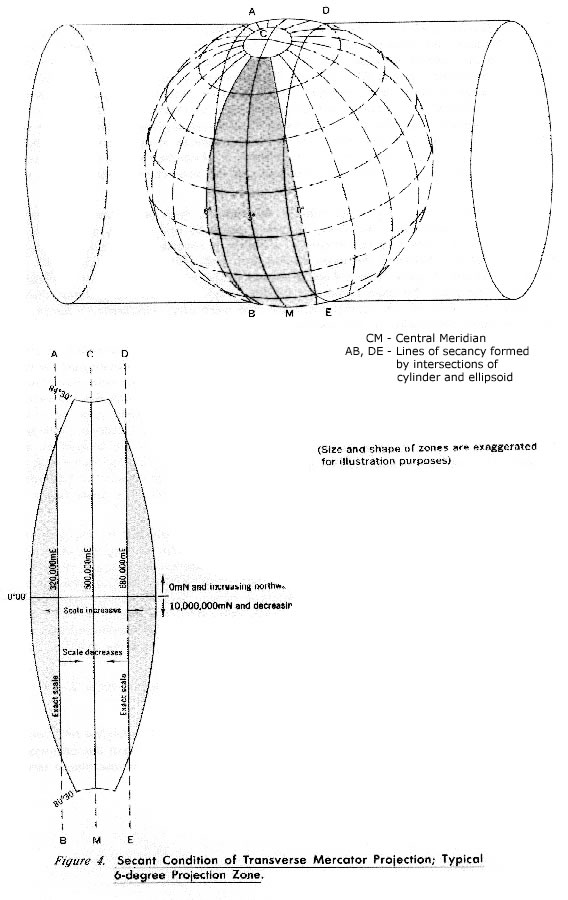
Et triks for å øke sonebredden og likevel ivareta nøyaktigheten er å skalere kartet noe. En skaleringsfaktor på 0.9996 er mye brukt. På sentermeridianen vil kartet vise for liten skala. 180km fra sentralmeridianen er skaleringen riktig, og lenger ut enn dette er skaleringen for stor. I eksempelet med observatoriet i Oslo som fundamentalpunkt fikk vi negativ verdi for øst. Det er ofte vanlig å sette en offsett slik at børe øst og nordverdien gir positive tall, for eksempel kan man legge til 500000 til østverdien, og la nordverdien ha nullverdi så lang syd at vi unngår negative verdier (f. eks ekvator).
Vi vil finne en rekke oppmålingssystemer som er basert på dette systemet, for eksempel NGO-48 (Norges geografiske oppmåling), RT-90 (Svensk rutenett), KKK-27 (Finsk rutenett), Nederlands grid, Engelsk rutenett, Belgisk rutenett osv.
UTM
Universal Transverse Mercator er et rettvinklet koordinatsystem som gir koordinater på hele jordkloden frp S80° til N84°. Man har valgt ut 60 sentralmeridianer og latt disse representere hvert sitt sonebelte.
Hvert sonebelte dekker 6 lengdegrader. Sone 1 går fra W180° til W174°. Sone 2 fra W174° til W168° osv. Sone 32 blir da fra E6° til E12° med sentermeridian i E9°. Sonebokstavene er egentlig ikke nødvendige, men for Norge bruker vi sonebokstav V mellom N56° og N64°, og W mellom N64° og N72°.
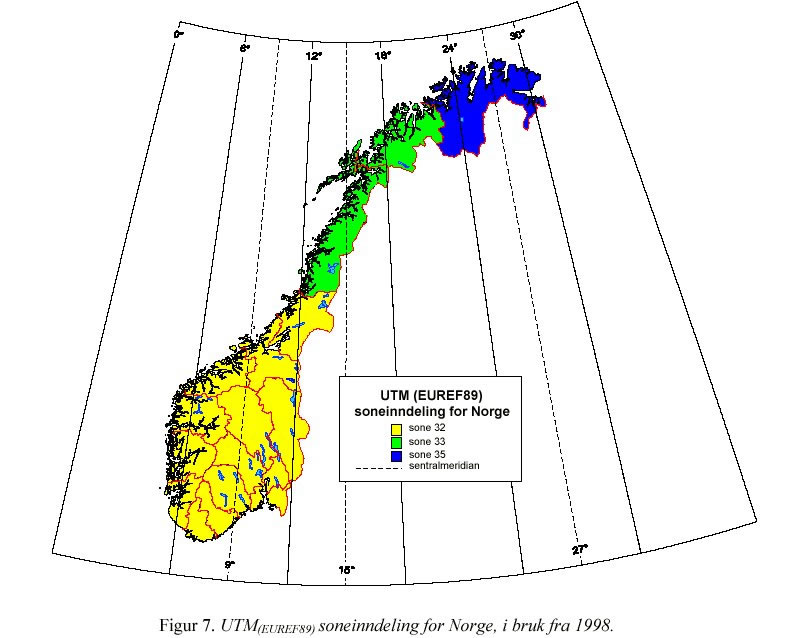
For et fullstendig sonekart se (HER).
I UTM systemet er skaleringsfaktoren 0.9996, har øst offset=500000 og bruker ekvator som nullpunkt for nord. I dette systemet ville Kragstøtten fått koordinatene 32V 592423 6649585, altså sone 32, 6649585m nord for ekvator langs E9° meridianen og vinkelrett østover 92423m.
I Norge skal posisjoner i Syd-Norge og Trøndelag angis med sone 32, Nordland og Troms i sone 33 og Finnmark i sone 35. Sone 34 skal ikke brukes. For kartverk som dekker hele landet, skal sone 33 brukes for hele Norge.
Hvilket datum
Stort sett kan GPS brukere i dag la være å tenke på datum.
Når man kjøper en GPS har den et fabrikkoppsett, og her er datum satt til WGS84.
Har man kart på GPSen er dette selvfølgelig tilpasset innstillingene
og hvilket datum man bruker er irrelevant. På www.geocaching.com sine sider
står det i bunn av alle sider: "Coordinates are in the WGS84 datum".
Likevel finnes innstillinger for å endre datum. Hvorfor?
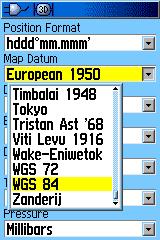 |
Hvis man på en Garmin 60C går inn i setup-menyen/units
finner man en meny som heter "Map Datum". Listen er lang og inneholder
en rekke uforståelige betegnelser, men vi kjenner igjen "WGS
84" og har sikkert også en ide om at "Timbalai 1948"
høres feil ut. Men hva med "Europeisk datum 1950"? |
For de som bor i nærheten av Oslo kan man følge veien fra Sognsvann
til Ullevållseter. Ved Store Åklungen ser man dette skiltet:
 |
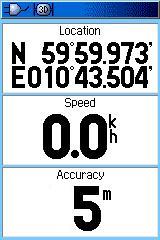
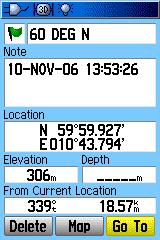
Men min GPS viser ikke 60 grader N. Det er lett å tro at den bommer
på 50m (eller skiltet er satt 50m for langt mot syd.). I virkeligheten
har vi satt vår GPS på feil datum. |
| På min GPS har jeg muligheten til å
vise posisjon i to datum samtidig, og jeg setter den opp til å vise
"WGS 84" øverst og "Europeisk datum 1950 (ED50)"
nederst. Hvis vi fikk oppgitt koordinater i ED50 og uten videre plugget
dem inn i vår GPS ville vi bommet med neste 100m (50m i n/S etening
og 80m i Ø/V retning). Andre steder i landet kan avviket være
større eller mindre. |
 |
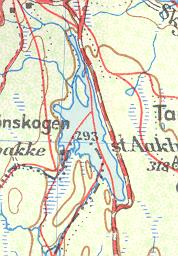 |
Mitt gamle nordmarkskart er oppmålt i 1938 og revidert
i 1968 (jeg har en nyere et også). Det er et koordinatkryss på
kartutsnittet og viser 60° nord og 0 meridianen. Hvis kartet hadde hatt
bedre målestokk og vi gikk inn og målte ville vi funnet
at skiltet sto på N59°59.927' E000°00.419'. Her er østlig
lengde målt relativet til nullmeridianen som går (gikk) gjennom
observatoriet i Oslo. Relativt til Greenwich vil koordinatene da bli N59°59.927'
E010°43.794'. Dette kartet er oppmålt i NGO-48. |
 |
På skolen lærte vi at man kunne angi en punkt med en koordinat,
breddegrad + lengdegrad. Eksempelet over viser at dette ikke er riktig. Man
må angi breddegrad + lengdegrad + datum. Dette er grunnen til at teksten
"Coordinates are in the WGS84 datum" på geocaching.com sine
web-sider.
Internt i en GPS/kartprogram lagres alle koordinater i WGS84 datum. Innstillingen
av datum på GPS/kartprogram er bare et filter som oversetter det man taster
inn fra det angitte datum til WGS84, og viser punktene lagret i GPSen i det
angitte datum.
Skal man plotte inn koordinater i sin GPS eller kartprogram MÅ GPS/kartprogram
settes til det datum koordinatene er registrer i, eller det datum kartet er
oppmålt med. GPS/kartprogram kan senere stilles om til WGS84 (eller annet
datum) uten at posisjonen endres.
| 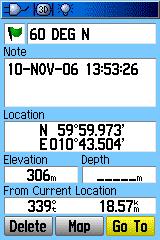
WGS84
|
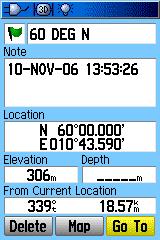
ED50
|
NGO-48
|
Waypointet ble satt ved å trykke MARK på GPSen.
Jeg kan ta fram Waypointet med ulik datumsetting og ser at koordinatene
er automatisk omregnet til riktig datum (med unntak av Øst-koordinaten
på NGO som er relativ til Greenwich, ikke Oslo). Avstand og retning
til punktet er et samme uavhengig av hvordan datum er satt på GPS.
|
Hvorfor er ikke N60° 00.000' det samme for alle datum?
Jordas form er nesten en perfekt kule, bare litt sammentrykket ved polene.
Jordas radius er ca 6380 km ved ekvator og ca 20 km mindre mot polene. Ser man
jorda fra verdensrommet ser det ut som en perfekt kule, men sammentrykkningen
ved polene gjør at den i virkeligheten er en elipsoide.
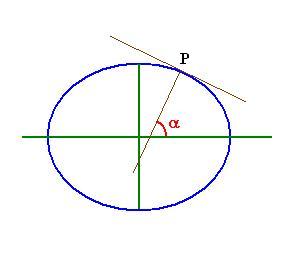
Et punkts geografiske bredde er definert som den vinkelen
ellipsoidenormalen i et punkt danner med ekvatorplanet. I figuren ser
vi at breddegrad i punktet P er vinkelen alfa.
I en figur hvor flattrykkingen av ellipsen hadde vært mindre ville
breddegraden for P blitt mindre. Hadde sammentrykningen vært større
ville breddegraden for P vært større.
|
 |
Hva er et datum?
Et datum er en beskrivelse av jordas form som sammen med et valgt fundamentalpunkt
(referanspunkt) danner en basis for måling og beregning av geografiske
data. Gitt en form og referansepunk kan alle posisjoner angis relativt til
dette. Det mest kjente fundamentalpunkt i verden er Greenwich observatoriet
nær London. I mange år var dette regnet som basis for alle kart,
men det var ikke mulig for land utenfor England å beregne avstand
fra 0-meridianen eksakt. Derfor har de fleste land et eller flere lokale
datum som kartene er tegnet etter. Ulike modeller for jordas form er også
prøvd ut. Man beskriver formen med:
a = Jordas radius ved ekvator
b = Jordas radus ved polene
f = (a-b)/a
Eksempler på ellipsoider (form) og datum (form + fundamentalpunkt):
| Ellipsoide |
a |
1/f |
Eksempel på datum |
| Bessel 1841 (Norge) |
6377492.0176 |
299.1528128 |
NGO-48 |
| Bessel 1841 |
6377397.155 |
299.1528128 |
RT-90 |
| Clarke 1866, |
6378206.4 |
294.9786982 |
North American datum-27 (NAD-27) |
| Clarke 1880, |
6378249.145 |
293.465 |
Hedgehog datum (Svalbard fram til 1948) |
| International 1924 |
6378388 |
297 |
European datum 1950 |
| Krassovsky 1940 |
6378245 |
298.3 |
Pulkovo 1942 (SR-42) |
| WGS 84 |
6378137 |
298.257223563 |
WGS 1984 |
Dette er bare et lite utvalg av Ellipsoider og datum som finnes. Totalt er
det minst 15 mer eller mindre brukte ellipsoider og et ukjent antall datum
som bygger på disse. Som eksempel tok jeg også med NAD-27 som
brukes over hele Nord-Amerika og SR-42 som dekker området som lå
under Sovjetunionen.
Litt historie

Det tidligst moderne kart over Norge ble tegnet av Claudius Clavus i Italia
omkring 1425 og dekket Syd-Skandinavia. Kartet over er en trykt utgave fra 1482
basert på dette kartet.
Kartvesenet lå først under det militæret, og ble etterhvert
til Norges Geografiske Oppmåling. I 1844 startet man oppmåling
av Syd-Norge basert på en Bessel 1841 ellipsoide. Fundamentlpunktet
for oppmålingen var Oslo Observatorium N59° 54' 44.00" E010°
43' 22.5". Omtrent samtidig startet oppmåling av Nord-Norge basert
på Fuglenes Datum 1850 med samme ellipsoide og fundamentalpunkt i Fuglenes
i Hammerfest N70° 40' 11.23" E023° 40' 12.8".
Historien sier at da Norge ble målt opp var Norges kopi av meteren
litt kortere enn originalen i Paris. Siden oppmålingen allerede var
gjort da dette ble oppdaget måtte man korrigere ellipsoiden for å
få oppmålingen til å stemme med "riktig" meter.
Derfor måtte store halvakse gjøres litt lengere enn den originale
Bessel ellipsoide. Derfor brukes ellipsoiden "Bessel 1841 (Norge)"
som er en Besselellipsoide korrigert for denne feilen.
Disse ble i 1948 slått sammen til et Nasjonalt datum, som har fikk
navnet NGO-48. Dette navnet fordi det var Norges Geografiske Oppmåling,
(som senere skiftet navn til Statens Kartverk) som etablerte dette som offisielt
datum i 1948.
Omtrent samtidig startet man i Europa et program for å måle opp
hele Europa i et Datum, og dette ble etablert som Europeisk Datum 1950 (ED50).
NATO krevde at alle militære kart skulle utgis på ED50 datum. Dermed
ble målet om å utgi alle kart i NGO-48 forlatt allerede i 1955,
og kartseriene M711 (1:50000) og M515 (1:1250000) etablert i ED50 datum. Også
sjøkartene ble trykt i ED50 datum, og i Nordsjøen er det fortsatt
ED50 som brukes.
Med innføring av satellittposisjonering ble det behov for et verdensdekkende
referansesystem, og World Geodetic System of 1984 (WGS-84) ble etablert. Nye
topografiske kart og sjøkart blir laget i EURREF89/WGS-84 datum, mens
økonomisk kartverk fortsatt i mange kommuner bruker NGO-84. EUREF89 som
er det samme som WGS-84 slik Norge ble målt opp i WGS-84 i 1989. EUREF89
kan litt forenklet sies å være en europeisk tilpasning av WGS84
og er låst til den kontinentalplaten som dekker Europa (og deler av Asia).
Vår kontinentalplate driver noen cm i året, noe som betyr at et
punkt flytter seg noen cm i året i WGS84 datum, mens det er fast i EUREF89.
Hvilket posisjonsformat?
 |
I omtalen av datum har jeg bare brukt geografiske koordinater
(lengde + breddegrader). Lengde og breddegrader refererer seg til
at jorda er rund, men innenfor mindre områder er det lettere
å betrakte område som ganske flatt. Derfor bruker man
vanligvis rettvinklete koordinater med meterangivelse når kartområdet
ikke er for stort.
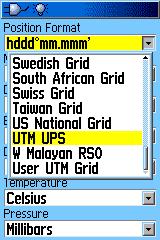
På alle GPSer vil man finne en meny for å velge mellom
ulike posisjonformat. Det er bare tre valg som er interessante for
oss, hdd°mm.mmm', UTM UPS og User UTM Grid. I Norge brukes hovedsaklig
UTM som er et rettvinklet koordinatsystem. På eldre økonomisk
kartverk finnes også NGO-48 tegnet ut i rettvinklede koordinater
men dette er i prinsippet konstruert på samme måte som
UTM. |
Lengde/bredde eller UTM?
| Vi bestemmer vår posisjon ved breddegrad og lengdegrad
og dette er også enerådende for navigasjon på sjø
og for flytrafikk, men på landjorda kan det være lettere
å tenke seg lokale områder som helt flate og hvor vi bestemmer
tenker oss et rettvinklet koordinatsystem lagt over bakken. Posisjonen
som i UTM-systemet skrives som 32V 0596214 6652617 betyr at vi befinner
oss i sone 32V, 96214m øst for meridianen E9° målt ovenfra
og 6652617m nord for ekvator målt langs jordbuen (og meg ulike datum
vil disse avstandene variere). Tilsvarende vil koordinater i NGO-48
sone3 referere seg til antall meter vest(-) eller øst(+) for
Oslo observatorium, og antall meter nord for 58°N. |

|
Hvorfor UTM?
I UTM er det svært lett å regne avstander. Siden verdiene viser antall
meter øst/vest for en referansemeridian og antall meter nord for ekvator
kan man ganske enkelt finne avstand mellom to punkter.

I dette kartutsnitet fra Kikut-kartet, Oslo skal vi legge merke til flere ting.
Rutenettet er blått. Det betyr at det er målt opp i WGS84-datum (eller
egentlig EUREF89). Hadde rutenettet vært sort hadde kartet vært oppmålt
i Europeisk Datum 1950, og vår GPS måtte stilles om til datum ED50 for
at avlesning på kartet skulle stemme med GPS.
Referanser:
1. Grunnleggende landmåling, Terje Skogsth, Universitetsforlaget.



